How to implement Binary Search and Tree Golang

Basic Definition

Data structure Binary Search and Tree is a pattern used for tree -based search. Before you further know Binary Search Tree commonly called BST, you need to first understand the concept of tree. Tree (tree) is a form of data structure that illustrates the hierarchical relationship between its elements (such as one to many relations). A node in a tree can usually have several more nodes as branching over him.

Then there is another name binary tree, what else is that? The concept is the same as Tree, it’s just that we will take the nature of binary numbers that are always worth 1 or 0 (2 choices). Means, Binary Tree is a tree that can only have a maximum of 2 branches.

So, Binary Search Tree is a sorted tree (order binary Tree) which has advantages when compared to other data structures. Among them are the sorting process and search (searching) can be done if the data has been arranged in the data structure BST. Sorting can be done if BST is traced (traversed) using the in-order method. The details of this search process will be discussed at the next meeting. Data that has been arranged in the BST data structure can also be found easily and has an average complexity of O (log n), but takes a time of o (n) In the ultimate condition where BST is not balanced and forms like a linked list.

Rules of Binary Search Tree

BST data structure has several rules so that it can be said to be like that, here are the rules:

• All data on the left of the sub-tree of Node T is always smaller than data in the T node itself.
• All data on the right of the sub-tree of Node T is always bigger or the same as the data in node t.

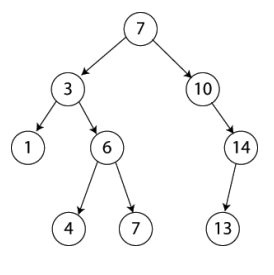
BST Here is a 9 BST with a depth of 3 with The leaf node (leaf) is 1, 4, 7 and 13.

Code Implementation

package main

type Tree struct {
	node *Node
}

func (t *Tree) insert(value int) *Tree {
	if t.node == nil {
		t.node = &Node{value: value}
	} else {
		t.node.insert(value)
	}
	return t
}

type Node struct {
	value int
	left  *Node
	right *Node
}

func (n *Node) insert(value int) {
	if value <= n.value {
		if n.left == nil {
			n.left = &Node{value: value}
		} else {
			n.left.insert(value)
		}
	} else {
		if n.right == nil {
			n.right = &Node{value: value}
		} else {
			n.right.insert(value)
		}
	}
}

func (n *Node) exists(value int) bool {
	if n == nil {
		return false
	}

	if n.value == value {
		return true
	}

	println("value ", n.value)
	if value <= n.value {
		return n.left.exists(value)
	} else {
		return n.right.exists(value)
	}
}

func printNode(n *Node) {
	if n == nil {
		return
	}

	println(n.value)
	printNode(n.left)
	printNode(n.right)
}

func main() {
	t := &Tree{}
	t.insert(10).
		insert(8).
		insert(20).
		insert(9).
		insert(0).
		insert(15).
		insert(25)

	// print all node
	printNode(t.node)
	// find exist
	println(t.node.exists(26))
}

10
8
0
9
20
15
25
value  10
value  20
value  25
false

Explanation

See from the implementation above, we know the concept of Binary Search Tree, that after we call Func Exists, seen the print results provide information that when printing we will explore the tree based on value and conditions. In the example of the code above, we will look for the value of 26 and we search in the data is not available because the value of 26 is not input or added to the tree.

Let’s see the search print, because the value of 26 is more than 10 and more than 20 and finally more than 25 then, the search is at 3 times the loop until it determines the point not found.